Przetwarzanie sygnałów towarzyszy każdemu człowiekowi codziennie. Wszystkie bodźce (sygnały) odbierane z otaczającego nas świata, tj. dźwięk, światło, temperatura są przetwarzane w impulsy elektryczne, przesyłane następnie do mózgu. Tam następuje analiza i interpretacja odebranych sygnałów, w wyniku której otrzymujemy informacje płynące z danego rodzaju sygnału (np. rozpoznajemy kształt przedmiotu, odczuwamy ciepło itp.).
W podobny sposób działa Cyfrowe Przetwarzanie Sygnałów (CPS). W tym przypadku sygnał analogowy konwertuje się na sygnał cyfrowy przez przetwornik analogowo-cyfrowy. Następnie przy użyciu komputera przetwarzane są dostarczone sygnały. W systemach CPS wykorzystuje się również komputerowe urządzenia peryferyjne, wyposażone w procesory sygnałowe, dzięki którym możliwe jest przetwarzanie sygnałów w czasie rzeczywistym. Niekiedy potrzebna jest ponowna konwersja sygnału do postaci analogowej (np. do sterowania jakiegoś urządzenia). W tym celu wykorzystuje się przetworniki cyfrowo-analogowe.
Cyfrowe przetwarzanie sygnałów ma bardzo szerokie zastosowanie. Może być wykorzystywane m.in. do przetwarzania dźwięku, rozpoznawania i przetwarzania mowy, czy do przetwarzania obrazów. To ostatnie zagadnienie będzie przedmiotem tego artykułu, a konkretnie omówimy w nim podstawową operację wykonywaną w procesie cyfrowego przetwarzania obrazów, tj. filtrację splotową.
Czym jest przetwarzanie obrazów?
Mówiąc w najprostszy sposób, przetwarzanie obrazów polega na przekształceniu obrazu wejściowego w obraz wyjściowy. Celem tego procesu jest selekcja informacji – wybranie najistotniejszych (np. kształtu) oraz wyeliminowanie zbędnych (np. szumów). Proces cyfrowego przetwarzania obrazów obejmuje szereg różnorodnych operacji, m.in.:
- filtrację,
- binaryzację,
- segmentację,
- transformację geometryczną,
- kodowanie,
- kompresję.
Jak już wspominaliśmy, w tym artykule omówimy szerzej operację filtracji obrazów.
Filtracja splotowa
Zarówno w domenie jednowymiarowej, przykładowo dla sygnałów audio, tak również dla dwóch wymiarów istnieją odpowiednie narzędzia służące przeprowadzeniu operacji na sygnałach, w tym przypadku na obrazach. Jednym z takich narzędzi jest filtracja. Polega ona na wykonaniu na pikselach obrazu wejściowego pewnych operacji matematycznych, w wyniku których otrzymywany jest nowy obraz. Najczęściej filtrację wykorzystuje się w celu poprawy jakości obrazu lub wydobycia z niego istotnych cech.
Podstawową operacją w metodzie filtracji jest operacja splotu 2D. Pozwala ona na aplikowanie przekształceń obrazu z użyciem odpowiednio przygotowanych do tego filtrów w postaci macierzy współczynników. Wykorzystanie filtrów polega na obliczeniu nowej wartości punktu na podstawie wartości punktów znajdujących się w jego otoczeniu. Do obliczeń wykorzystuje się tzw. maski, zawierające wagi pikseli z otoczenia danego piksela. Najczęściej spotykane rozmiary masek to 3×3, 5×5 i 7×7. Poniżej przybliżono proces przeprowadzenia konwolucji obrazu oraz filtra.
Przyjmując, że obraz reprezentowany jest przez macierz o wymiarach 5×5, zawierającą wartości kolorów, a filtr reprezentowany macierzą 3×3, przeprowadzono modyfikację obrazu poprzez splecenie jednej z nich z drugą.
Pierwsze, co należy wykonać to zamiana wierszy, a następnie kolumn w macierzy filtra (wiersz/kolumna pierwsza → wiersz/kolumna ostatnia – i na odwrót). Należy również przyjąć, że środek jądra filtracji h(0,0) znajduje się w środku macierzy, tak jak to pokazano na poniższym rysunku. W związku z taką konwencją indeksy (m,n) oznaczające wiersze i kolumny macierzy filtra będą ujemne i dodatnie.
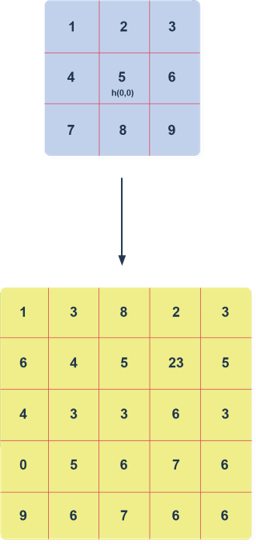
Uznając macierz filtra (kolor niebieski) za odwróconą w pionie i poziomie, możemy przeprowadzić operację filtracji. Dokonujemy tego umieszczając element h(0,0) → h(m,n) macierzy niebieskiej w elemencie s(-2,-2) → s(i,j) macierzy obrazu (kolor żółty). Następnie wymnażamy nachodzące na siebie wartości obu macierzy i sumujemy. W ten sposób otrzymaliśmy wynik splotu dla komórki o(-2,2) obrazu wyjściowego.
Kolejne etapy procesu są analogiczne, przesuwamy środek macierzy niebieskiej do elementu s(-2,-1), wymnażamy nachodzące na siebie wartości, sumujemy, otrzymując wynik wyjściowy. Pola, które wykraczają poza obszar macierzy s(i,j) uznajemy za niezdefiniowane, w związku z tym wartości w tych miejscach nie istnieją, a więc nie dokonujemy mnożenia.
Zastosowanie filtracji splotowej
W zależności od rodzaju filtra wyróżnia się różne zastosowania filtracji splotowej. Filtry dolnoprzepustowe wykorzystywane są do usuwania szumów w obrazach, natomiast filtry górnoprzepustowe stosowane są do wyostrzania lub podkreślenia krawędzi.
W celu zobrazowania działania poszczególnych rodzajów filtrów spróbujmy zastosować praktyczny przypadek konwolucji na rzeczywistym obrazie. Poniższy obraz w formacie „.jpg” został wczytany jako macierz MxNx3 pikseli. Na jego przykładzie pokażemy podstawowe efekty możliwe do uzyskania, dzięki zastosowaniu filtracji splotowej.

Rozmycie Gaussowskie
Aby dokonać rozmycia obrazu należy zastosować funkcję splotu, jak również odpowiednio przygotowany kernel – filtr. Jednym z najczęściej wykorzystywanych do tego filtrów dolnoprzepustowych jest filtr Gaussowski. Pozwala on na zmniejszenie ostrości obrazu, jak również stosuje się go przy redukcji szumu obecnego w obrazie.
W prezentowanym przypadku wykorzystano macierz o wymiarach 29×29, wygenerowaną na podstawie funkcji Gaussowskiej o odchyleniu standardowym równym 5. Rozkład normalny nadaje wagi otaczającym pikselom w procesie konwolucji. Działanie filtra dolnoprzepustowego polega na tłumieniu elementów obrazu charakteryzujących się wysoką częstotliwością i przepuszczaniu tych elementów, których częstotliwość jest mała. W rezultacie następuje redukcja szumów oraz rozmycie obrazu, a otrzymany obraz jest mniej wyraźny niż pierwotny.

Wyostrzanie
Analogicznie jak przy rozmyciu Gaussowskim można sprawić, że obraz zostanie wyostrzony. W tym celu należy zastosować odpowiedni filtr górnoprzepustowy. Jego działanie polega na przepuszczaniu oraz wzmacnianiu elementów obrazu, które odznaczają się dużą częstotliwością, np. szumów czy krawędzi. Natomiast elementy o małej częstotliwości filtr wytłumia. W wyniku zastosowania filtru następuje wyostrzenie pierwotnego obrazu, co można łatwo zauważyć na przykład w okolicach ramienia.

Detekcja krawędzi
Kolejnym zabiegiem możliwym do przeprowadzenia przy użyciu filtracji splotowej jest detekcja krawędzi. Do przeprowadzenia operacji wykrywania krawędzi wykorzystuje się filtry przesuwania i odejmowania. Ich działanie polega na przesunięciu obrazu i odjęciu obrazu pierwotnego od jego kopii. W wyniku tej operacji następuje detekcja krawędzi.

BFirst.Tech a przetwarzanie obrazów
Jako firma posiadamy wykwalifikowaną kadrę, a także doświadczenie w dziedzinie cyfrowego przetwarzania obrazów.
Projektem, do realizacji którego wykorzystano przetwarzanie obrazów, jest platforma Webowa Virdiamed. Została ona stworzona we współpracy z firmą Rehasport Clinic. Platforma polega na rekonstrukcji 3D danych pochodzących z tomografu komputerowego, a także z rezonansu magnetycznego. Umożliwia ona podgląd danych 3D w przeglądarce internetowej. Więcej informacji o naszych projektach znajdziesz tutaj.
Cyfrowe przetwarzanie sygnałów, w tym także przetwarzanie obrazów, jest dziedziną techniki o szerokich możliwościach stosowania, a jej popularność ciągle rośnie. Nieustający postęp technologiczny sprawia, że również ta dziedzina cały czas się rozwija. Wiele technologii stosowanych na co dzień działa w oparciu o przetwarzanie sygnałów, dlatego też pewnym jest, że w przyszłości znaczenie CPS będzie ciągle rosnąć.
Bibliografia
[1] Leonowicz Z.: „Praktyczna realizacja systemów DSP”
[2] http://www.algorytm.org/przetwarzanie-obrazow/filtrowanie-obrazow.html